Properties of Matrix Operations
Properties of Addition
The basic properties of addition for real numbers also hold true for matrices.
Let A, B and C be m x n matrices
- A + B = B + A
commutative
- A + (B + C) = (A + B) + C
associative
- There is a unique m
x n matrix O
with
A + O = A additive identity
- For any m
x n matrix A
there is an m x n matrix
B (called -A)
with
A + B = O additive inverse
The proofs are all similar. We will prove the first property.
Proof of Property 1
We have
(A + B)ij = Aij + Bij definition of addition of matrices
= Bij + Aij commutative property of addition for real numbers
= (B + A)ij definition of addition of matrices
Notice that the zero matrix is different for different m and n. For example

Properties of Matrix Multiplication
Unlike matrix addition, the properties of multiplication of real numbers do not all generalize to matrices. Matrices rarely commute even if AB and BA are both defined. There often is no multiplicative inverse of a matrix, even if the matrix is a square matrix. There are a few properties of multiplication of real numbers that generalize to matrices. We state them now.
Let A, B and C be matrices of dimensions such that the following are defined. Then
- A(BC) = (AB)C
associative
- A(B + C) = AB + AC
distributive
- (A + B)C = AC + BC
distributive
- There are unique matrices Im
and In with
Im A = A In = A multiplicative identity
We will often omit the subscript and write I for the identity matrix. The identity matrix is a square scalar matrix with 1's along the diagonal. For example
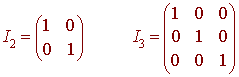
We will prove the second property and leave the rest for you.
Proof of Property 2
Again we show that the general element of the left hand side is the same as the right hand side. We have
(A(B + C))ij = S(Aik(B + C)kj) definition of matrix multiplication
= S(Aik(Bkj + Ckj)) definition of matrix addition
= S(AikBkj + AikCkj) distributive property of the real numbers
= S AikBkj + S AikCkj commutative property of the real numbers
= (AB)ij + (AC)ij definition of matrix multiplication
where the sum is taken from 1 to k.
Example
We will demonstrate property 1 with
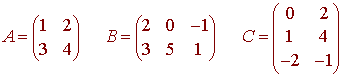
We have
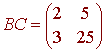
so that
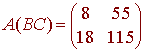
We have
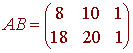
so that
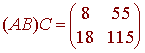
Properties of Scalar Multiplication
Since we can multiply a matrix by a scalar, we can investigate the properties that this multiplication has. All of the properties of multiplication of real numbers generalize. In particular, we have
Let r and s be real numbers and A and B be matrices. Then
- r(sA) = (rs)A
- (r + s)A = rA + sA
- r(A + B) = rA + rB
- A(rB) = r(AB) = (rA)B
We will prove property 3 and leave the rest for you. We have
(r(A + B))ij = (r)(A + B)ij definition of scalar multiplication
= (r)(Aij + Bij) definition of addition of matrices
= rAij + rBij distributive property of the real numbers
= (rA)ij + (rB)ij definition of scalar multiplication
= (rA + rB)ij definition of addition of matrices
Properties of the Transpose of a Matrix
Recall that the transpose of a matrix is the operation of switching rows and columns. We state the following properties. We proved the first property in the last section.
Let r be a real number and A and B be matrices. Then
- (AT)T = A
- (A + B)T = AT
+ BT
- (AB)T = BTAT
- (rA)T = rAT
Back to the Matrices and Applications Home Page
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions