Math 203 Practice Midterm 3

Please work out each of the given problems.  Credit will be based on the steps towards the final answer.  Show your work.  Do your work on your own paper.

Problem 1

A physicist has plotted the position of a projectile over time.  Based on Newton’s laws, the projectile should ideally travel in a parabolic path.  Use matrices to find the most likely equation of this parabola.  (You may use a calculator, but show the matrices that are being manipulated).

Solution

We consider the matrix and vector

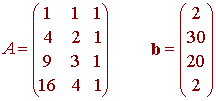
Then we solve the system

        A^TAx  =  A^Tb 

which becomes

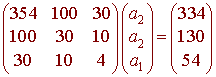
We now rref the corresponding augmented matrix

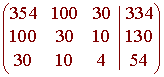
to get

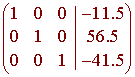
We can conclude that the least squares regression parabola is given by

        y  =  -11.5x² + 56.5x - 41.5

Problem 2

A new species of fish is introduced into the Truckee River.  Initially 2 fish were stocked.  It takes one year for this species to spawn, when each fish averages 3 successful children each year.  (So there are 2 at the beginning, 2 at the end of the first year, 8 at the end of the second year, 14 at the end of the third year, etc.)

A.     Assuming no fish die, set up a recursion relationship that gives the number of fish w_n at the end of year n.

Solution

        We have that the number of fish should be the number previous plus the offspring of those two years ago.  We get

                w_n  =  w_n-1 + 3w_n-2

                w_n-1  =  w_n-1

B.     Find a matrix A such that w_n-1  =  A^n-1 (w₀, w₁)^T .

Solution

        We can write the recursive equation as 

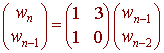
        The above 2 x 2 matrix is what is required.

C.     Find a diagonal matrix D such that A is similar to D.

    Solution

        We need to find the eigenvalues and eigenvectors for A.  First for the eigenvalues.  We have

        det(A - lI)  =  (1 - l)(-l) - 3  =  l² - l - 3  =  0

        has roots 

        The diagonalized matrix is 

Problem 3

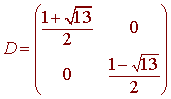
Let V be the subspace of differentiable functions spanned by {e^x, e^2x, e^3x} and let

        L:  V --->  V

be the linear transformation with 

        L(f(x))  =  f ''(x) - 3f '(x) + 2f(x)

A.     Write down the matrix A_L with respect to the given basis.

Solution

        We have

                L((1,0,0)  =  L(e^x)  =  e^x - 3e^x + 2e^x  =  0  =  (0,0,0)

                L((0,1,0)  =  L(e^2x)  =  4e^2x - 6e^2x + 2e^2x  =  0  =  (0,0,0)

                L((0,0,1)  =  L(e^3x)  =  9e^3x - 9e^3x + 2e^3x  =  2e^3x  =  (0,0,2)

        The matrix of L is the matrix whose columns are the vectors above.

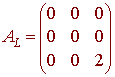
B.     Find the a basis for the kernel and range of L.

              Solution

                    A basis for the kernel corresponds to the null space of A_L which has basis 

                            {(1,0,0), (0,1,0)}

                    in other words the basis is given by

                        {e^x, e^2x}

Problem 4 

Let W = Span{(1,1,0,1), (0,1,2,3)}.  Find a basis for the orthogonal complement of W.

  Solution

        The orthogonal complement is equal to the null space of the matrix whose rows are the given vectors.  If 

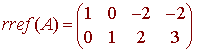
        then the rref(A) is given by

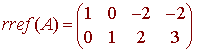
        so that a basis for the null space is given by

                {(2,-2,1,0), (2,-3,0,1)}

Problem 5

Let 

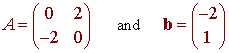
and T be the affine transformation T(x)  =  Ax + b .  Sketch the image under T of the figure below.

 Solution

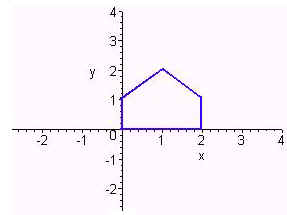
We just compute T(x) for each of the vertices and use the theorem that under an affine transformation line segments go to line segments.  We have

        T(0,0)  =  (0,0) + (-2,1)  =  (-2,1)        T(2,0)  =  (0,-4) + (-2,1)  =  (-2,-3)

        T(2,1)  =  (2,-4) + (-2,1)  =  (0,-3)       T(1,2)  =  (4,-2) + (-2,1)  =  (2,-1)

        T(0,1)  =  (2,0) + (-2,1)  =  (0,1)

The image is shown below in red.  Notice that this is a rotation by -p/2 then a expansion by a factor of 2 then a translation by (-2,1)

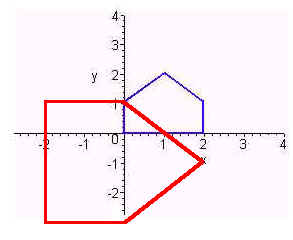
Problem 6

Let  L:  V ---> V  be a linear transformation.  Use the fact that 

        dim(Ker L) + dim(Range L)  =  dim(V)

to show that if L is one to one then L is onto. 

Solution

  If L is one to one then the kernel of L is just the zero vector space since only zero gets sent to zero.  Hence 

        dim(Ker L)  =  0

The equation tells us that

        dim(Range L)  =  dim(V)

Since the range is a subspace of V and has the same dimension as V, the range of L equal V.  We can conclude that L is onto.

Problem 7 

Let A and B be matrices and let v be an eigenvector of both A and B.  Prove that v is an eigenvector of the product AB.

Proof

  If v is an eigenvector of A and B, then there are numbers a and b with

        Av  =  av          and            Bv  =  bv  

We then have

        (AB)v  =  A(Bv)  =  A(bv)  =  b(Av)  =  bav  =  abv 

Hence v is an eigenvector of AB with eigenvalue ab.

Problem 8

Answer True of False and explain your reasoning.

A.    Let A be a 3x3 matrix such that the columns of A form an orthonormal set of vectors.  Then

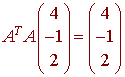
Solution

True, since A is an orthogonal matrix, we have 

        A^T  =  A^-1 

so that

        A^TA  =  A^-1A  =  I

B.     Let V be the vector space of continuous functions then the expression

        <f, g>  =  f(1) + g(1)

defines an inner product on V.

False, for example if 

        f(x)  =  -x 

then

        <f, f>  =  f(-1) + f(-1)  =  -1 + -1  =  -2  <  0

violating the first property of inner products.