Math 203 Practice Midterm 2
Please
work out each of the given problems. Credit
will be based on the steps towards the final answer.
Show your work.
Problem 1
Let L: R2 --> R3 be a linear transformation such that
L
(1,4) = (1,-1,3)
and L
(0,2) = (2,1,4)
Find L(1,0)
Problem 2
Of the following two
subsets of the vector space of differentiable functions, determine which is a
subspace. For the one that is not a
subspace, demonstrate why it is not. For
the one that is a subspace, prove that it is a subspace.
A.
S = {f | f(3) = f '(3)}
B.
T = {f | f(0)f '(0) = 0}
Problem 3
Let S
= {t2, t2 + 2t, t2 + 3}
and T
= {2t - 1, 5t - 3, t2}
be subsets of P2
A.
Prove that S is a basis for P2.
B. Find the transition matrix PS<--T.
Problem 4
Suppose that you want to
change the graphic file from the one on the left to the one on the right.
What is the matrix needed to adjust the pixels appropriately?
Assume the center of the picture is the origin.
Problem 5
Let
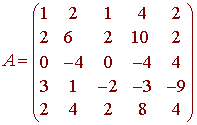
A. Find the rank and the nullity of A.
B. Find a basis for the Null Space of A.
C. Find a basis for the Column Space of A using columns of A.
D.
Find a basis for the Row Space of A
using rows of A.
Problem 6
Let S = {v1, v2, ..., vn} be a set of linearly independent vectors and let v be a vector in the span of S. Prove that v can uniquely be written as a linear combination of elements of S. That is that prove that if
v = a1v1
+a2v2 + ... + anvn
and
v
= b1v1
+b2v2 + ... + bnvn
then
a1 = b2, a2 = b2,
... , an = bn

