Math 203 Practice Exam 2
Please work out each
of the given problems. Credit will
be based on the steps towards the final answer.
Show your work. Do your work
on your own paper.
Problem 1
Let S
= {t2, t2 + 2t, t2 + 3}
and T
= {2t - 1, 5t - 3, t2}
be subsets of P2
A.
Prove that S is a basis for P2.
B. Find the change of basis matrix PS<--T.
Problem 2
Of the following two
subsets of the vector space of differentiable functions, determine which is a
subspace. For the one that is not a
subspace, demonstrate why it is not. For
the one that is a subspace, prove that it is a subspace.
A.
S = {f | f(3) = f '(3)}
B.
T = {f | f(0)f '(0) = 0}
Problem 3
Let
V be the subspace of differentiable functions
spanned by {ex, e2x, e3x}
and let
L: V
---> V
be the linear transformation with
L(f(x)) = f ''(x) - 3f '(x) + 2f(x)
A. Write down the matrix AL with respect to the given basis.
B. Find the a basis for the kernel and range of L.
Problem 4
Let W
= Span{(1,1,0,1), (0,1,2,3)}. Find
a basis for the orthogonal complement of W.
Let
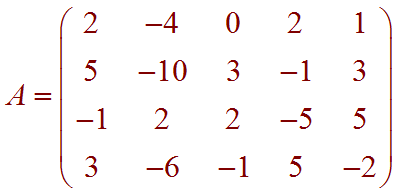
Find the following:
-
A basis for the column space of A.
-
A basis for the row space of A.
-
A basis for the null space of A.
-
The nullity of A.
-
The rank of A.
Problem 6
Let L: V ---> V be a linear transformation. Use the fact that
dim(Ker L) + dim(Range L) = dim(V)
to show that if L
is one to one then L is onto.
Problem 7
Let A
and B be matrices and let v
be an eigenvector of both A and B.
Prove that v
is an eigenvector of the product AB.
![A = Matrix[ (2,6),(6,7)]](img9.gif)
Problem 9
Answer True of False and
explain your reasoning.
A. Let A be a 3x3 matrix such that the columns of A form an orthonormal set of vectors. Then
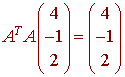
C. If u and v are eigenvectors for a matrix A, then u + v is also an eigenvector for A.
D. If A is similar to B and B is similar to C, then A is similar to C.
E. If l is an eigenvalue for A, then l2 is an eigenvalue for A2.
F. The vectors (1,1,0), (1,0,1), and (0,0,1) are a basis for P2.