Comparing, Ordering and Rounding Decimals

1. Comparing Decimals
   
   At the beginning of this course, we we encountered the number line, a graphical device that helps us visualize the relationships between two numbers.  Just as we can place whole numbers on the number line, we can also place decimals on the number line.  If two numbers are on a number line, then the number to the right is the larger one.  
   
   
   
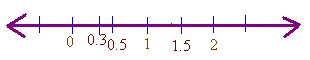
   We see that that 
   
           0.5 < 2        and     0.3 < 0.5
   
   To compare two decimals without placing them on a number line, follow the following method:
   
   
   1. Start from left to right and compare corresponding digits.  If the digits are the same, move to the right.
      
   2. If the digits are different then the larger number is the one with the larger digit.
      
      

   Example

   Fill in the blank with a "<", ">", or an "=" sign

    

   1. 3.1714        3.169
      
      Solution
      
      We see that the ones digits, 3 and 3, are the same, the tenths digit, 1 and 1 are the same, but the hundredths digits, 7 and 6, are different with 7 > 6.  Hence the inequality is ">"
      
      3.1714  >  3.169
      
      
   2. 0.0005        0.0023
      
      Solution
      
      We see that the ones digits, the tenths digits, and the hundredths digits are all 0.  The left hand side has 0 for the thousandths digit while the right hand side has 2 for its thousandths digit.  Hence the inequality is "<"
      
      0.0005  <  0.0023
      
      

   Exercises

   Fill in the blank with a "<", ">", or an "=" sign

    

   1. 34.916        34.924       
      
   2. 18.126        18.1260       
      
   3. 123.437          123.337       
      
      

   Example
   
   Place the following decimals from in order from smallest to largest
   
           2.753    2.75    2.357    3    2.7
   
   Solution

   We first add zeros to the ends of the shorter decimals to make comparison easier

           2.753    2.750    2.357    3.000    2.700

   Now we see that the smallest is 2.357, since its tenths digit, 5, is smaller than 5.  Next is 2.700, since its hundredths digit, 0, is smaller than 5.  Next comes 2.750 since its thousandths digit, 0, is smaller than 3.  
   

   Example
   
   Place the following decimals from in order from smallest to largest
   
           49.1        49.16        49.31        27    49.01
   
   
   
   

2. Rounding Decimals to a Specified Decimal Place

   It is often necessary to round a decimal to the nearest tenth, hundredth, thousandth, etc.  When dealing with money we usually round to the nearest hundredth so that we can read the number in dollars and cents.  The rules of rounding decimals are the same as the rules for rounding whole numbers.  We look at the digit to the right and determine if it is 5 or greater.  If it is greater than 4, round up.  Otherwise round down.

   
   
   Example

   Round 32.537 to the nearest hundredth.

    

   Solution

   The digit to the right of the hundredth place is "7".  Since 7 is greater than 4, we round up.  Change the 3 to a 4.  We write

           32.54

    

   Example

   Round 27.8149 to the nearest tenth.

    

   Solution

   The digit to the right of the tenth place is "1".  Since 1 is not greater than 4, we round down.  Keep the 8 the same.  We write

           27.8

   Exercise

   Round the following numbers as indicated.

   1. 651.955 to the nearest tenth       
      

   2. 49.942 to the nearest hundredth   

Back to the Decimals page

Back to the Math 187A page

Back to the Math Department page

e-mail Questions and Suggestions