Circles and Distance
The Distance Formula
Recall that the Pythagorean Theorem states that if a, b, c are sides of a right triangle with c the hypotenuse, then
a2 + b2 = c2
Let (x,y) be a point in the plane. Then if we draw the triangle with one vertex at the origin, one at (x,y) and one at (x,0) then we have a right triangle which has one leg of length x and the other of length y. The length of the hypoteneuse is the distance from the origin to the point (x,y). By the Pythagorean Theorem, this distance is
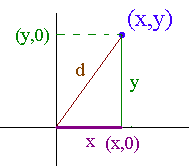
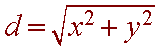
Exercise:
Find the distance from the origin to the point (5,12)
![]()
We can generalize this notion to find the distance between two points (x1,y1) and (x2,y2)
We draw the triangle and see that the length of its legs equal
x2 - x1 and y2 - y1
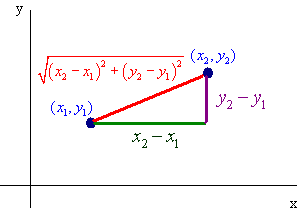
Therefore the distance from (x1,y1) to (x2,y2) is
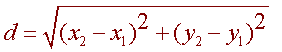
Example
Find the distance from (2,-3) to (-1,4)
Solution:
We use the distance formula:
![]()
Recall that a circle with radius r and center (h,k) is defined by the set
of point of distance r from the point (h,k). If
(x,y) is on the circle
then the distance from (h,k) to (x,y) is
r. The distance formula tells
us that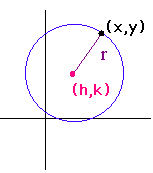
(x - h)2 + (y - k)2 = r2
This is called the standard form of the equation of the circle.
Example
The equation of the circle with radius 3 centered at (1,2) is
(x - 1)2 + (y - 2)2 = 9
Example: Find the center and radius of the circle
x2 + y2 - 4x + 6y - 12 = 0
We must get the equation into standard form by completing the squares. We have
x2 - 4x + y2 + 6y = 12
-4/2 = -2 and 6/2 = 3
(-2)2 = 4 and 32 = 9
Adding and subtracting we have
x2 - 4x + 4 - 4 + y2 + 6y + 9 - 9 = 12
(x - 2)2 + (y + 3)2 = 12 + 4 + 9 = 25 = 52
So that the center of the circle is (2,-3) and the radius is 5.
Click here to interactively practice graphing a circle.
Back to the Intermediate Algebra (Math 154) Home Page