Ellipses and Hyperbolae
Draw an Ellipse With a String and Two Fixed Points
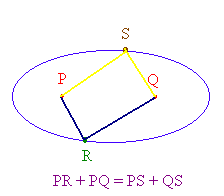
Geometrically an ellipse is defined as follows: Let P
and Q be fixed points in the plane and let k be
a positive real number. Then a point R is in the ellipse if the sum of
the distances from P to R
and from Q to R is
k
PR + QR = k
For an interactive view of this concept click here
http://www.nationalsciencecenter.org/FortDiscovery/Robotics/demos/ellipse/EllipseApplet.htm
The Standard Form of an Ellipse Centered at The Origin
Recall that the equation of a circle centered at the origin has equation
x2 + y2 = r2
where r is the radius. Dividing by r2 we have
x2
y2
+
=
1
r2
r2
for an ellipse there are two radii, so that we can expect that the denominators should be different. Hence we have the standard form of an ellipse centered at the origin:
x2
y2
+
=
1
a2
b2
The points (a,0), (-a,0), (0,b), and (0,-b) are called the vertices of the ellipse.
Note: Although we have written the a below the x and the b below the y, it is customary to let a be the larger of the two and b be the smaller.
Example
Graph the ellipse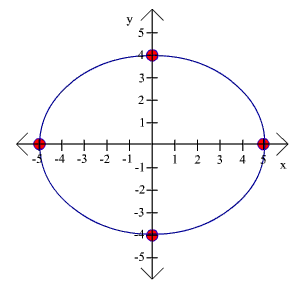
x2
y2
+
= 1
25
16
Solution
First identify a and b, remembering to take square roots.
a = 5 b = 4
Next plot the vertices
(-5,0), (5,0), (0,4), and (0,-4)
Finally, connect the dots. The graph is shown to the right.
Example
Graph the ellipse
4x2 + y2 = 16
Solution
This is not in standard form since the right hand side is not 1. To rectify this, we just divide by 36 to get
4x2
y2
+
= 1
16
16
or since 9/36 = 1/4, we get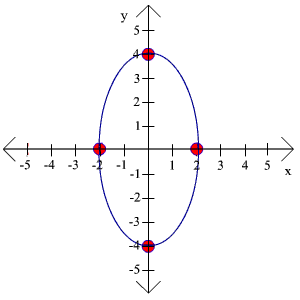
x2
y2
+
= 1
4
16
Now we can sketch the graph. Notice that 16 is larger than 4 so we let a be the square root of 16 and b be the square root of 4. We have
a = 4 and b = 2
We plot the vertices
(0,4), (0,-4), (2,0), and (-2,0)
and connect the vertices with a conic as shown to the right.
Example
Graph the ellipse
4x2 + 9y2 = 4
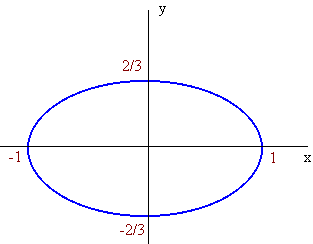
Solution:
First divide by 4
x2 + 9/4y2 = 1
Since the 9/4 is not in the denominator, we need to use the following fact about division of numbers
9
1
=
4
4/9
This comes from looking at the right hand side and and noticing that it is just a division of the fraction 1/1 by 4/9, which becomes a multiplication of 1/1 by 9/4.
x2
y2
+
=
1
1
4/9
so that
a = 1 and b = 2/3
Application: Astronomy
Suppose that an asteroid orbits the sun (in an elliptical orbit). And suppose that the longest opposite ends of the orbit are 800 million miles apart and that the shortest opposite ends are 200 million miles apart. Give an equation for the orbit of the asteroid.
Solution:
We have
2a = 800 million miles
and
2b = 200 million miles
thus
a = 400 million miles and b = 100 million miles
so that
x2
y2
+
=
1
(400,000,000)2
(100,000,000)2
The Hyperbola
Recall the equation of the ellipse:
x2
y2
+
=
1
a2
b2
If instead of a "+" we have a "-", we end up with a different conic called the hyperbola.
x2
y2
-
=
1
a2
b2
Example
Sketch the graph of
x2
y2
-
=
1
4
9
Solution
Check for intercepts:
If x = 0 then
y2
-
= 1 which has no solution
9
If y = 0 then
x2
= 1
4
x2 = 4
so that
x = 2 or x = -2
If instead of the 1, we have a 0 then
x2
y2
-
=
0
4 9
so that
x2
y2
=
4
9
hence
y = (3/2)x or y = -(3/2)x
These two lines are called the asymptotes of the hyperbola and are found by
y = ![]() b/a
b/a
To plot the hyperbola with equation
x2
y2
-
=
1
a2
b2
we follow these steps:
-
Plot the intercepts
(a,0), (-a,0)
and the points
(0,b), (0,-b)
as with the ellipse.
-
Draw a rectangle containing these four points.
-
Draw the lines that contain the diagonals of the rectangle (these are the asymptotes)
-
Draw the hyperbola that with the vertices
(a,0) and (-a,0)
that has the drawn asymptotes.
Following these steps, to sketch the graph of