Solutions to the Odd Problems on Hyperbolae Centered at the Origin

1.  For the hyperbola

              x²            y²    
                     -                  =  1
             9              4

the vertices are at the points  (-3,0) and  (3,0) .

3.  The asymptotes of the hyperbola 

              x²            y²    
                     -                  =  1
             9              4

have equations y = -2/3 x  and  y = 2/3 x .

5.  The graph of 4x² - 25y² =  36 is not a hyperbola since the right hand side is not equal to 1.

True, since hyperbolae do not pass the vertical line test.

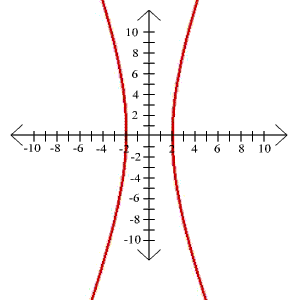
7.          x²            y²    
                     -                  =  1
             4             36

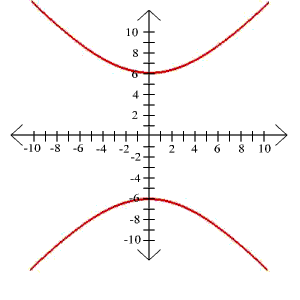
9.          y²            x²    
                     -                  =  1
            36             25

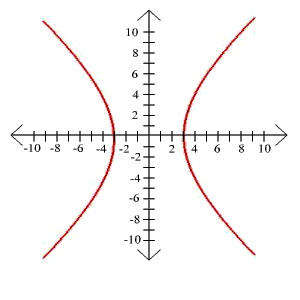
11.         x²          
                     -   y²       =  1
             9              

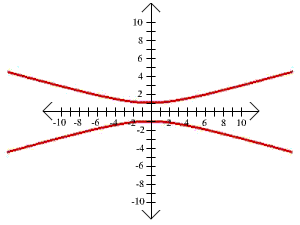
13.                       x²    
            y²   -                  =  1
                          7

15.         x²          
                     -   16y²       =  1
             4         

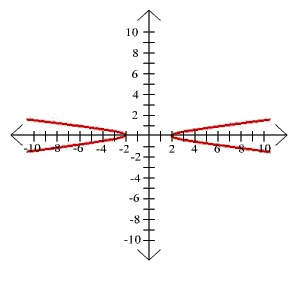
17.      y²   -   16x²   =  1

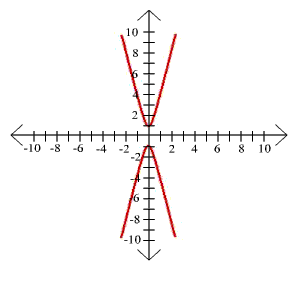
19.     100x²   -   81y²   =  1

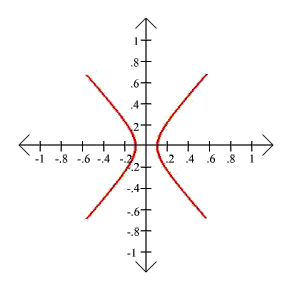
21.     18x²   -   11y²   =  1

23.     9y²   -   x²   =  36

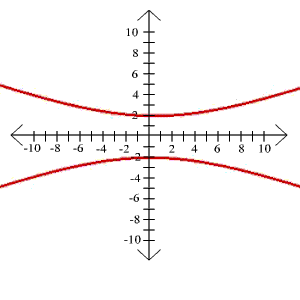
25.     25x²   -   4y²   = 100

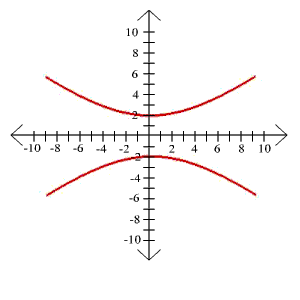
27.     16y²   -   x²   =  25

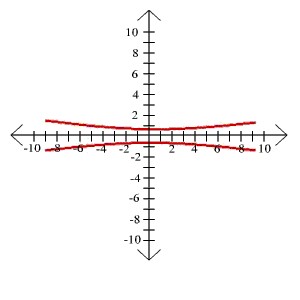
29.     36x²   -   25y²   =  49

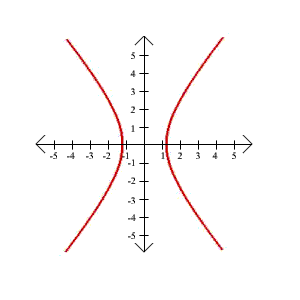
31.     4y²   -   64x²   =  8

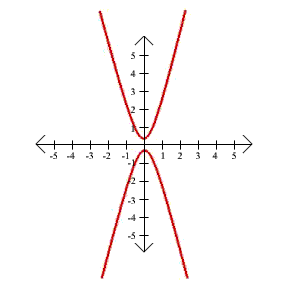
33.     6x²   -   15y²   =  9

35.  A hyperbola centered at the origin has vertices (0,-5) and (0,5) and passes through the point ( , 10).  Find its equation.

             y²          
                     -   x²       =  1
             25              

37.    Hyperbola

39.    Line

41.    Parabola      

Back to the Exercises

Back to The Conic Page

Back to the Math 154 Page

Back to the Math Department Home Page