Name                          .

Math 152B Midterm I

Please do all of the following problems.  Credit earned will be based on the steps that you show that lead to the final solution.  Good Luck!

Problem 1:  Factor the expression completely:

A)   x⁴ - 9x²  

Solution:  x²(x² - 9)

B)    x² + 3x - 54  

Solution:  (x + 9)(x - 6)

C)    6x² + 11x - 10  

Solution: AC = -60, gives (15, -4)

            6x² + 11x - 10 = 6x² + 15x - 4x - 10   

            =  3x(2x + 5) - 2(2x + 5)  =  (3x - 2)(2x + 5)

D)    128xyz³ + 54x⁴y  

Solution:  2xy(64z³ + 27x³)  =  2xy(4z + 3x)(16z² - 12xz + 9x²)

Problem 2:  Perform the indicated operations and express your answer in simplest form.

A       2x² - x - 1     x² - 6x + 8
                           ^.                                            
         x² - 5x + 4    2x² - 3x -2

              (2x + 1)(x - 1)     (x - 4)(x - 2)
   =                                ^.                               =   1                   
             (x - 4)(x - 1)        (2x + 1)(x - 2)

B       x² + 2 xy + y²           y + x
                                                                 
          x² - x - 2                x - 2

                   x² + 2xy + y²      x - 2
        =                              ^.                                    
                   x² - x - 2             y + x

                   (x + y)(x + y)         x - 2
        =                               ^.                                    
                     (x - 2)(x + 1)       x + y

                    (x + y)    
        =                                               
                    (x + 1)  

Problem 3:  Solve the following equations

A.   x³ - 2x² + x = 0  

Solution:  First factor

            x(x² - 2x + 1) = 0

            x (x-1)²  =  0
    Now use the zero property 

            x = 0     or     x = 1

B.    4x² = 15 - 4x

  Solution:  4x² + 4x - 15 = 0

               AC  =  -60:   (10, -6)

        4x² + 4x - 15  =  4x² + 10x - 6x - 15

        =  2x(2x + 5) - 3(2x + 5)  =  (2x - 3)(2x + 5)  =  0

        2x - 3  =  0     or      2x + 5  =  0

        x = 3/2    or    x = -5/2

Problem 4:  Solve the following inequalities

A.     |4 - 3x|  < 2  

Solution:  4 - 3x  =  2    or     4 - 3x  =  -2

                -3x  =  -2    or    -3x  =  -6

                x  =  2/3    or    x  =  2

                [2/3, 2]

B.  |3x + 1| < 0  

 Solution:   3x + 1  =  0,    x  =  -1/3

Problem 5:  There is a lookout post situated in the center of a 3 mile circular trail.  How far is the lookout post from the trail?

 Solution:  

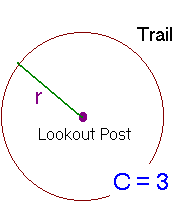
The circumference formula gives

                     C = 2pr   where 

                    C  =  the circumference (3 miles)

        and 

                    r = the radius (the distance from the lookout post to the trail)

                    3  =  2pr  

        divide by 2p  

                    r = 3/2p  

        The distance from the lookout post to the trail is 3/2p  miles.

Problem 6:  Please answer the following true or false and explain your reasoning.

A.  If all terms of a trinomial are positive, all terms of both binomial factors will be positive

Solution:  True, (under the convention that the first coefficient if the first factor is always positive.)

B.  The solution to the inequality |x - 4|  <  -1 is the interval [3,5].

  Solution:  False,  The absolute value can never be negative, hence there is no solution.