Parametric Equations

Lines

Recall that a line has equation 

        y  =  mx + b  

Suppose that one airplane moves along the line 

        y  =  2x + 3

while the other airplane moves along the line 

        y  =  3x - 2

       
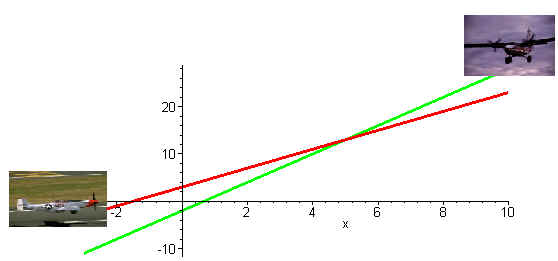
Can you tell whether the airplanes collide?  Even though the lines intersect, the equations themselves do not tell us whether there will be a mid air collision.  To be able to mathematically model this scenario, we use parametric equation.  We introduce the variable t for time and write x and y as a function of t.  

Consider the two sets of equations:

1. x(t) = t,       y(t) = 2t + 1 
   

2. x(t) = 2t,     y(t) = 4t + 1

These describe the same line, but the second one travels twice as fast.

Definition  A curve given by            x = x(t), y = y(t)  is called a parametrically defined curve and the functions            x = x(t) and y = y(t)  are called the parametric equations for the curve.

Finding the Parametric Equations for a Line Given Two Points

Example:  

Find the parametric equations for the line through the points (3,2) and (4,6) so that when t = 0 we are at the point (3,2) and when t = 1 we are at the point (4,6).

Solution:  

We write symbolically: 

        (x,y)  =  (1 - t) (3, 2)+ (t) (4, 6) 

        =  (3 - 3t + 4t, 2 - 2t + 6t)  =  (3 + t, 2 + 4t)

so that 

        x(t)  =  3 + t     and     y(t)  =  2 + 4t

Functions

If y = f(x) is a function of x we can write parametric equations by writing

        x  =  t      and      y  =  f(t).

Example  

The parabola  

        y = x²  

can be represented by the parametric equations:

        x  =  t     and     y  =  t²

Circles

Consider the circle centered at (0,0) with radius 2.  We can write it parametrically as

        x(t)  =  2cos(t)     and     y  =  2sin(t)

We see that the circle is drawn in a counterclockwise direction.  We can draw the same circle as

        x(t)  =  2cos(-t)     and     y(t)  =  2sin(-t)

now the circle is drawn clockwise.  We can also write

        x(t)  =  2 cos(t²)     and     y  =  2 sin(t²)

now the circle begins slowly and speeds up.

A Cool Example

The graph of 

         x(t) = 11cost - 6cos(11/6 t)      and      y(t) = 11sin(t) - 6sin(11/6 t)

is pictured below:

       

Eliminating the Parameter

If a curve is given by parametric equations, we often are interested in finding an equation for the curve in standard form:  

        y = f(x)

Example

Consider the parametric equations

        x(t) = t²     and     y(t) = sin(t)      for  t  >  0

To find the conventional form of the equation we solve for t:


        t =  

hence

        y = sin()

is the equation.

Example

Eliminate the parameter for

        x(t)  =  e^t     and     y(t)  =  e^2t + 1


Solution

We write:

        y(t)  =  (e^t)² + 1

Hence 

        y = x² + 1

Intersections

Let 

        x₁(t)  =  2t + 1     and     y₁(t)  =  4t²  

and 

        x₂(t)  =  3t      and      y₂(t)  =  3t

Do they intersect?  If so then there is a c with

        2c + 1  =  3c
 
and 

        4c²  =  3c

the first equation gives us that 

        c  =  1

Putting this into the second equation we have

        4  =  3 

which tells us that they do not intersect.  Do their graphs intersect?  If so then there exists a c and a k such that

        2c + 1  =  3k 

and 

        4c²   =  3k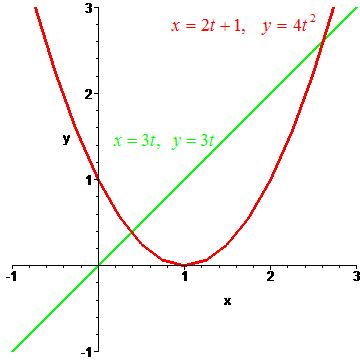

Hence, we see that

        2c + 1  =  4c²  

or that

        4c²  - 2c - 1  =  0

We solve to get two intersection points

       

 

hence their graphs intercept.  Their graphs are shown on the right.

Back to the Polar and Parametric Equations Page

Back to the Math 107 Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions