Tangent Planes and Normal Lines
Tangent Planes
Let z = f(x,y) be a function of two variables. We can define a new
function F(x,y,z) of three variables by subtracting
z. This has the
condition
F(x,y,z) = 0
Now consider any curve defined parametrically by
x = x(t),
y = y(t) z = z(t)
We can write,
F(x(t), y(t), z(t)) =
0
Differentiating both sides with respect to t, and using the chain rule gives
Fx(x, y, z) x' + Fy(x,
y, z) y'
+ Fz(x, y, z) z' = 0
Notice that this is the dot product of the gradient function and the vector
<x',y',z'>,
GradF .
<x', y', z'> = 0
In particular the gradient vector is orthogonal to the tangent line of any
curve on the surface. This leads to
|
Definition Let F(x,y,z) define a surface that is differentiable at a point (x0,y0,z0), then the tangent plane to F ( x, y, z ) at ( x0 , y0 , z0 ) is the plane with normal vector Grad F(x0,y0,z0) that passes through the point (x0,y0,z0). In Particular the equation of the tangent plane is Grad F(x0,y0,z0) . < x - x0 , y - y0 , z - z0 > = 0 |
Example
Find the equation of the tangent plane to
z = 3x2 - xy
at the point (1,2,1)
Solution
We let
F(x,y,z) = 3x2 - xy - z
then
Grad F = <6x - y,
-x, -1>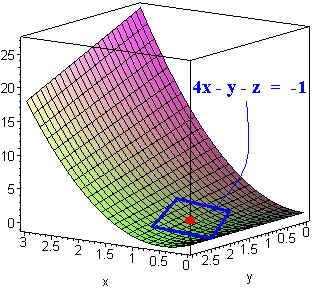
At the point (1,2,1), the normal vector is
Grad F(1,2,1) = <4, -1, -1>
Now use the point normal formula for a plan
<4, -1, -1> .
<x - 1, y - 2, z - 1> = 0
or
4(x - 1) - (y - 2) - (z - 1) =
0
Finally we get
4x - y - z = 1
Normal Lines
Given a vector and a point, there is a unique line parallel to that
vector that passes through the point. In the context of surfaces, we
have the gradient vector of the surface at a given point. This leads
to the following definition.
|
Definition |
Example
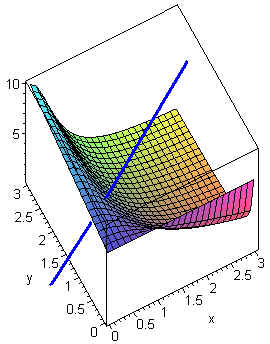
Find the parametric equations for the normal line to
x2yz - y
+ z - 7 = 0
at the point (1,2,3).
Solution
We compute the gradient
Grad F = <2xyz, x2z -
1, x2y + 1> = <12, 2, 3>
Now use the formula to find
x(t) = 1 + 12t
y(t) = 2 + 2t z(t) = 3 + 3t
The diagram below displays the surface and the normal line.
Angle of Inclination
Given a plane with normal vector n the angle
of inclination, q is defined by
|
|n .
k| cosq = ||n|| |
More generally, if
F(x,y,z) = 0
is a surface, than the angle of
inclination at the point (x0, y0,
z0)
is defined by the angle of inclination of the tangent plane at the point.
|
|Grad F(x0, y0, z0)
. k| cosq = ||Grad F(x0, y0, z0)|| |
Example
Find the angle of inclination of
x2
y2
z2
+
+
= 1
4
4 8
at the point (1,1,2).
Solution
First compute
Grad F = <x / 2, y /
2, z / 4>
Now plug in to get
Grad F(1,1,2) = <1/2,
1/2, 1/2>
We have
|<1/2, 1/2, 1/2> .
k| = 1/2
Also,
||<1/2, 1/2, 1/2>|| =
![]() / 2
/ 2
Hence
cosq =
(1/2)/[(![]() )/2] =
1/
)/2] =
1/![]()
So the angle of inclination is
q =
arccos(1/![]() ) @
0.955 radians
) @
0.955 radians
The Tangent Line to a Curve
Example
Find the tangent line to the curve of intersection of the sphere
x2 + y 2 +
z2 = 30
and the paraboloid
z = x2 + y2
at the point (1,2,5).
Solution
We find the Grad of the two surfaces at the point
Grad (x2 + y 2
+ z2) = <2x, 2y, 2z> = <2, 4,10>
and
Grad (x2 + y 2
- z) = <2x, 2y, -1> = <2, 4, -1>
These two vectors will both be perpendicular to the tangent line to the
curve at the point, hence their cross product will be parallel to this
tangent line. We compute
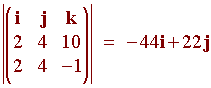
Hence the equation of the tangent line is
x(t) = 1 -
44t
y(t) = 2 + 22t z(t) = 5
Back to the Functions of Several Variables Page
Back to the Math 107 Home Page