Related Rates

Related Rates

Another synonym for the word "derivative" is "rate" or "rate of change".  When you hear the word "rate" you should identify d/dt, since rate always corresponds to the derivative with respect to time.  

To solve a related rate problem you should do to following:

1. Draw the picture (if applicable).
   

2. Identify what derivatives are known.
   

3. Identify what derivative is asked for.
   

4. Find an equation that relates only the variables for which the derivatives are known and the variable for which the derivative is asked for.
   

5. Implicitly take the derivative with respect to t (apply d/dt to both sides of the equation).
   

6. Plug in all known constants.
   

7. Answer the question.
   

Example 

Suppose a bird is flying horizontally 40 feet above your head at 20 ft/sec.  How fast is the angle of elevation changing when your horizontal distance from the bird is 30 feet?

Solution:  

1. We draw the picture.   
   
   
   
   

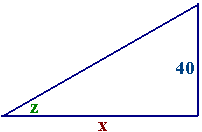
2. We know 
   
           dx/dt = 20 ft/sec
   
   

3. We want to find dz/dt.  
   
   

4. Using the triangle we get
   
                         40
       tan(z)  =               
                          x
   
   

5. Taking derivatives we have that
   
           sec²(z) dz/dt = -40x ^-2 dx/dt
   
   

6. We use the Pythagorean theorem to find the hypotenuse given that x is 30.
   
           c²  =  30² + 40²
   
           c  =  50

   Hence 
   
           sec(z) = 50/30  =  5/3
   
   Plugging in we get:
   
            25     dz            -40
                               =             20
             9      dt             900        

             dz            -40       9                 -8
                     =                      20  =            rad/min
            dt             900      25               25

   
   

7. The angle is decreasing at 8/25 rad/min.
   
   

Exercises

1. The included area of the two sides of equal length s of an isosceles triangle is z.  If z is increasing at a rate of 1/3 radians per minute, find the rate of change of the area when z = p/6.
   

2. A spherical balloon is increasing at a rate of 5 inches per minute.  Find the rate of change of the volume when r = 3 inches.
   

3. At a sand and gravel plant, sand is falling off a conveyor and onto a conical pile at the rate of 20 cubic feet per minute.  The diameter of the base of the cone is approximately three times the altitude.  At what rate is the height of the pile changing when it is 10 feet high?
   

4. A boat is pulled by means of a winch on the dock 12 feet above the deck of the boat.  The winch pulls in rope at the rate of  3 feet per second.  Determine the speed of the boat when there is 13 feet of rope out.  

Back to Math 105 Home Page

e-mail Questions and Suggestions