Epsilon-Delta
The Formal Definition of the Limit
|
e-d Definition of a Limit Let f(x)
be a function and L
be a
number we say that
if for any choice of e,
the d team can respond with a positive
number d so that with a "perfect
calculator" the d
team will win.
That is for any |
Example:
Show that if
f(x) =
7x
then
![]()
Solution:
Let
0 < e
Scratch Work:
we need to find a d such that
14 - e < f(x) < 14 + e
for all
2 - d
< x < 2 + d
or equivalently
14 - e < 7x < 14 + e
or after dividing by 7,
2 - e/7 < x < 2 + e/7
If we choose
d
= e/7
then
2 - e/7 < x < 2 + e/7
implies that
14 - e < 7x < 14 + e
so that
14 - e < f(x) < 14 + e
which proves that the limit is14.
Exercise
Prove that
A) If
f(x) = 3 - 5x
then
![]()
B) if
f(x) = mx + b
is a line then
![]()
A Proof of a Limit that Does Not Exist
Example:
Prove that the function

does not have a limit at x = 2
Solution:
Let
e =
.5
then for any chosen d, chose
m = min(d/2,0.01)
so that
f(2 - m)
= (2 - m)2 - 1 = 3 - 4m + m2 <
3.1
and
f(2 + m) = (2 + m) + 3 = 5 + m > 4.9.
Now for any L either
|3.1 - L| > 0.5 or | 4.9 - L| > 0.5
hence the limit does not exist. Below is the graph.
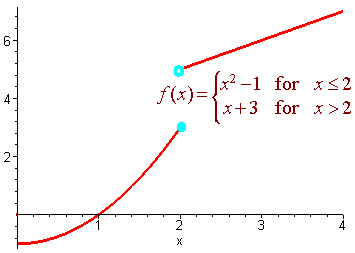
Notice that on the left hand side the limit approaches 3 and on the right hand side it approaches 5.
Exercise:
Prove that if
| f(x) = { | 3x - 5 for x < 1 |
| 2x + 2 for x > 1 |
then the limit does not exist.
Limits and Graphs
If f(x) is a function, then the limit as x approaches c is L if the y coordinates of the left hand side from x = c of the graph and the right hand side of the graph both approach L. Graphically, we can get a good guess of what the limit is by putting the function into a graphing calculator and checking to see if the left and right agree and the y coordinate is likely to be the limit. Once we have a guess of what the limit is, we can use the epsilon-delta definition to attempt to prove that what the calculator indicated is indeed the limit. For most functions and values of c, the conjecture that the calculator investigation produces will turn out to be correct; however, occasionally the calculator will produce misleading results.
Other Sites About Limits
Weisstein's World of Mathematics