Asymptotes

Definition of a Limit at Infinity

Definition of a Limit at Infinity Let L be a real number and f(x) be a function.  Then if for every e  > 0, there is an M > 0 such that  |f(x) - L| < e whenever x > M.

In other words as x gets very large f(x) gets very close to L.

If

then we say that y = L is a horizontal asymptote of f(x).

Example

Find the horizontal asymptote of

                           x² - 1
        f(x)  =                            
                       2x² + x - 3

Solution:

Divide by x² on the numerator and the denominator to get

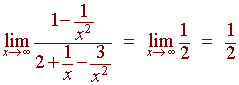
Horizontal Asymptotes of Non-Rational Functions

Example

Find the horizontal asymptotes of

       

Solution

We must consider the negative infinity case separately from the positive infinity case.  First note that for negative x,

       

hence
       
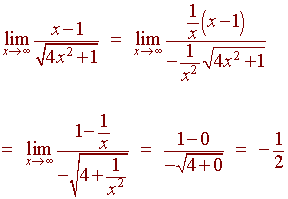
Next for positive,

       

hence
       

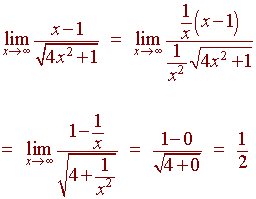
We see that there is a left horizontal asymptote at y = -1/2 and a right horizontal asymptote at y = 1/2.

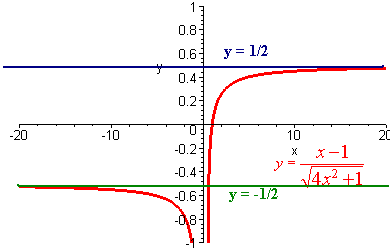
Example

Find the horizontal asymptotes of

                     sin x
        f (x)  =                   
                       x



Solution

We see that

             1          sin x           1
         -        <              <           
             x            x               x


for all x.  Both of the outer limits approach 0 as x approaches either infinity or negative infinity.  By the squeeze theorem, the middle limit must approach zero. We can conclude that f has a horizontal asymptote at y = 0.

Back to Math 105 Home Page

e-mail Questions and Suggestions