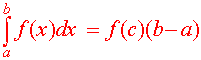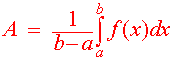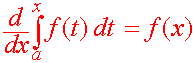The Second Fundamental Theorem of Calculus
The Mean Value and Average Value Theorem For Integrals
|
The Mean Value Theorem For Integrals Let f be continuous on [a,b], then there is a c in [a,b] such that
|
We define the average value of f(x) between a and
b as
|
Definition of the Average Value
|
Example
The average value of
y = sin x
between x = 0 and
x = p is
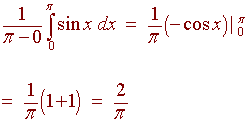
The Second Fundamental Theorem of Calculus
|
The Second Fundamental Theorem of Calculus Let f be continuous on [a,b] then
|
Eample

Example:
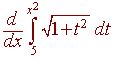
Solution
This is not in the form where second fundamental theorem
of calculus can be applied because of the x2. We use the chain
rule so that we can apply the second fundamental theorem of calculus.
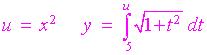
Example
Find the derivative of
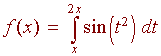
Solution
Here, the "x" appears on both limits. We use two properties of integrals to write this integral as a difference of two integrals.
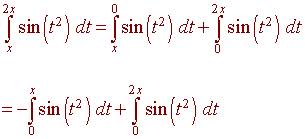
The first integral can now be differentiated using the second fundamental theorem of calculus,
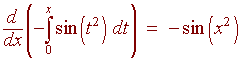
The second integral can be differentiated using the chain rule as in the last example.
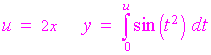
so that
![]()
Putting these results together gives the derivative of
2 sin(4x2) - sin(x2)
Click here for a challenge problem