Sequences and Series

1. Sequences

   Example:  Find the next term and describe the pattern:

    

   1. 2, 4, 6, 8, 10, ...
      

   2. 1, 4, 9, 16, 25, ...
      

   3. 3, 7, 15, 31, 63, ...
      

   4. 1, -1/2, 1/6, -1/24, 1/120, -1/720, ...

    

   Solution:

    

   1. We see that the next term is 12.  We can get to the next term by adding two.
      

   2. The next term is 36.  The terms are all squares.
      

   3. The next term is 127.  These numbers are all one less than a power of two.
      

   4. The next term is 1/5040.  The numbers alternate sign and the denominators are all factorials.

   
   

   Definition   A sequence is a list of numbers.  In technical terms, a sequence is a function whose domain is the set of natural numbers and whose range is a subset of the real numbers.

    

   Example:

   
   Consider the function 
   
           f(n) = 2n + 1  

   This function describes the sequence
   
           3,5,7,9,11,...
   
   We will usually use the notation a_n to describe a sequence instead of the notation f(n).

   
   

2. Finding the General Element of a Sequence 
   
   One technique for finding the general element a_n is to list the numbers 1,2,3,4,5,6... above the sequence and decide what do we have to do to the number 5 for example to get the fifth term.  then generalize.

    

   Example

   Find the general element a_n in the exercises listed above.

   
   
   Solution:

    

   1. a_n = 2n
      

   2. a_n = n² 
      

   3. a_n = 2ⁿ⁺¹ - 1
      

   4. a_n = (-1)ⁿ⁺¹ /n!

   
   

3. Recursively Defined Sequences

   A recursively defined sequence is a sequence where the first term(s) are given and the next term is given in terms of the previous terms.

    

   Example

   
   Let 
   
           a₁ =1,     a₂ = 1     

   and     

           a_n = a_{n - 1} + a_{n - 2}

   
   This is called the Fibonacci sequence and the terms are
   
           1,1,1+1 = 2,1+2 = 3,2+3 = 5,3+5 = 8,5+8 = 13,8+13 = 21,...
   
           1,1,2,3,5,8,13,21,34,55,...

   
   

4. Sigma Notation and Series

   
   

   Definition We define a series to be the sum of the sequence.

    

   Example:  

   
   If 
   
           1,1/2,1/4,1/8,... 
   
   is a sequence, then
   
           1 + 1/2 + 1/4 + 1/8 + ...
   
   is the corresponding sum.  We define the n^th partial sum as
   
           s_n =  a₁ + a₂ + a₃ + ... + a_n

   We write this series in Sigma Notation as follows.  

      

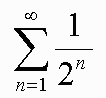
   This is read, "The sum from 1 to infinity of 1 over 2 to the n."

   Application:  
           e^x = 1 + x + x²/2!   x³/3!  ... xⁿ/n! + ... =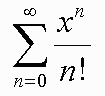

Back to the College Algebra Part II (Math 103B) Site

Back to the LTCC Math Department Page

e-mail Questions and Suggestions